Virtual Kid's Rule

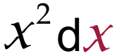
this means the integration is all about the X - for now, don't worry about what the d means.

This is what all the fuss is about - so we'll discuss it in this lower half of the page.

In this discussion of integration, we'll be talking about two letters - x and y. We will also use the word, "axis". One way to think about all these things at once, is to think about a cat being chased by a dog. The cat runs in a direction along the ground, that direction, whatever the direction is, can be thought of as the "x-axis". All of the sudden, the cat notices that the dog is beginning to catch up, but there is a tree just ahead. Just as the dog is about to catch the cat, the cat changes direction and heads up into the tree. We can think about the tree as the "y-axis". Axis, just means "some direction" - any direction. The x and y, indicate "which direction", and in this example, the x direction is along the ground, and the y direction is up the tree.

To help you remember which axis is which, remember about the cat and the tree. The Y kinda looks like a tree, and it represents the Y axis. Have you ever made a "snow angel by laying in the snow on your back and moving your arms along the ground between your head and your waist? The X is kinda like you laying on the ground making a "snow angel". So when you think about the X, think about you laying on the ground making the snow angel, or the cat running along the ground being chased by the dog. The X axis is along the ground, or horizontal, and the Y axis is up the tree, or vertical.

Now that you know what the x and y represent, for now, I'm just going to talk more about the x, but you need to remember about the y for a later discussion.

For those who don't already know, if a number, for example a 2 looks like 2² it means 2x2, and is usually referred to as 2 "squared". Because of x being used in math for other things than to mean "multiply", the x is usually replaced with the * symbol, so 2x2 becomes 2*2. For this calculus example you will also need to know what 2³ means, which is 2*2*2, or 2 cubed. You may also find it interesting that 2² can be found on the "Kid's Rule!" on the A scale. Try to find 2² on the slide rule now. All you need to do is put the cursor over the 2 on the D scale and up on the A scale you'll see 4.

One last thing you'll need to know about x, is that it is used kinda like you might use one of those "sticky-notes" that you can write something on and stick on your refrigerator to remind you of something. The x is just waiting for you to give it something to do. In this example, we are going to ask it to pretend like it's the number 1 for a while, and then we are going to ask it to pretend like it's the number 4. When it's the number 1, it will have an easy job because 1² is the same thinkg as 1*1, and that is just 1. When it's the 4, it's job will be a little harder because then, it will become 4² which means 4*4 which is 16 - a little harder to figure out, but still pretty simple for you, since you've already made it this far into the lesson.

That was a lot to comprehend, so you probably should study everything here again, think about it for a few days, and then click the link below go to the next page.

Click HERE to go to the next page.

This page explains the use of the symbols and things like x and dx. They can really make things look difficult, while their job is actually to prevent things from looking difficult.

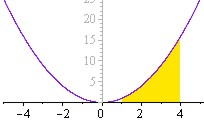
This is known as a "plot of the x² function. The part that's colored yellow, is the integration. It is the area beneath the curve between points 1 and 4.

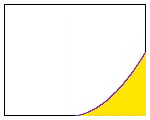
We can figure out how much cheese can be stashed below the dented corner of this square box.

That is really just
another way to think
about it. This kind of
math could be really
important to a mouse!

This is a square
with a dent in one
of the corners.

If this square was 8" x 8", and didn't have the big dent in the corner, we would know that the area inside of the square is 64 square inches. But now with calculus, we can even calculate the area inside a square that has a dent in the corner! All we need to do is to calculate the area in the dented area and then subtract that from the 64.

Did you notice that the dent in the box is the same shape as a portion of the x² curve? We can use any piece of any curve that we want to calculate areas of unusual shapes.

note: click the left mouse button anywhere on the screen to close this box, and then wait for it to fade away completely before again moving the mouse.

information about this will be here later.

note: click the left mouse button anywhere on the screen to close this box, and then wait for it to fade away completely before again moving the mouse.

Explanations will be here soon.