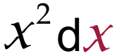

|
The last page was some pretty difficult stuff, mostly because there was a whole lot of new things to think about. As a refresher, remember
that x is just waiting to become something, for example, 1 or 4 (or any other number for that matter). If you replace the x in x2
with 4 then it becomes 42 which means "4 squared", which is the same thing as 4*4. To find 42 on the slide rule, you
just have to put the cursor over the 4 on the D scale and follow the red line up to the A scale and you'll see 16. Now all that is left to learn is how to do the integration. There are lots of ways to "integrate" in calculus, but for this example, we are going to use a simple technique. Using this technique is as simple as changing the x2 to x3 and then divide the answer by 3 for both of the numbers - the lower limit and the upper limit. Finally we need to subtract one from the other. To start things off, lets work on the lower limit which is 1. Replace the x2 with 13 (remember that we add 1 to 2 making it 3), which is the same as 1*1*1, and which has an answer of 1. We then need to divide that by 3. Lets do that on the slide rule first. The neat thing about dividing 1 by anything on the slide rule is that the answer can be found on the D scale below the number on the CI scale. In other words, you don't even have to move the slide. Just put the cursor over the CI:3 and below it find D:.333. You need to remember that number. Next, lets work on the upper limit which is 4. Replace the x2 with 43, which is the same as 4*4*4, and which has an answer of 64. We then need to divide that by 3. We are going to do a special trick for this one, so that we only need to move the slide once to do the entire process of 4*4*4 divided by 3. We are going to do the division first since we are allowed to do that when multiplying and dividing. So, we need to put C:3 over D:4. We can see the answer to that division below C1, but we aren't really interested in the answer because right away, we are going to multiply it by the 4*4 (which is 16) and we can find the answer below C:16 which is 21.333. The final step to this integration is to subtract the first number (.333) from the second number (21.333), which is something you can easily do in your head, giving a final answer of 21. That is the area below the x2 curve between the lower limit of 1 and upper limit of 4. Now, let's finish this thing about the box, cheese, and the mouse, with something that you may need to think about a while. Remember that we got 21.333... for the upper limit integration? That was the integration between the 0 and 4 limit - the interval within those limits. That is the actual area occupied by the cheese beneath the corner of the box. So, if the box is 8*8 (64), to get the area inside the box, all we need to do is subtract the 21.33... from the 64 which gives us an answer of approximately 42.67. Click HERE to go to the next page, showing a similar integration on the slide rule. |
| This page explains how to do the integration of x2 with a lower limit of 1 and an upper limit of 4. The result is the area beneath the curve. In other words, it is the amount of space occupied by the cheese below the corner of the box on the previous page. Well, almost the space, since it's beginning at 1 and not zero, there is still a little space not accounted for. We'll talk more about that later. |
|
note: click the left mouse button anywhere on
the screen to close this box,
and then wait for it to fade away completely
before again moving the mouse. information about this will be here later. |
|
note: click the left mouse button anywhere on
the screen to close this box,
and then wait for it to fade away completely
before again moving the mouse. Explanations will be here soon. |
|
note: click the left mouse button anywhere on
the screen to close this box,
and then wait for it to fade away completely
before again moving the mouse. Explanations will be here soon. |
|
note: click the left mouse button anywhere on
the screen to close this box,
and then wait for it to fade away completely
before again moving the mouse. Explanations will be here soon. |